Calculo Diferencial: 2014

viernes, 5 de diciembre de 2014

Funciones Trigonometricas

En matemáticas, las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de lasrazones trigonométricas a todos los números reales y complejos.

Las funciones trigonométricas son de gran importancia en física, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras muchas aplicaciones.

Las Razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.

Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométricamente o por medio de sus relaciones. Algunas funciones fueron comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan actualmente ; por ejemplo el verseno (1 − cos θ) y la exsecante (sec θ − 1).

Función	Abreviatura	Equivalencias (en radianes)
Seno	sin (sen)	$\sin \; \theta \equiv \frac{1}{\csc \theta} \equiv \cos \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\cos \theta}{\cot \theta} \,$
Coseno	cos	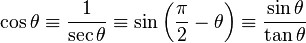$\cos \theta \equiv \frac{1}{\sec \theta} \equiv \sin \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\sin \theta}{\tan \theta} \,$
Tangente	tan	$\tan \theta \equiv \frac{1}{\cot \theta} \equiv \cot \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\sin \theta}{\cos \theta} \,$
Cotangente	ctg (cot)	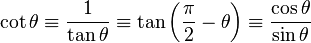$\cot \theta \equiv \frac{1}{\tan \theta} \equiv \tan \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\cos \theta}{\sin \theta} \,$
Secante	sec	$\sec \theta \equiv \frac{1}{\cos \theta} \equiv \csc \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\tan \theta}{\sin \theta} \,$
Cosecante	csc (cosec)	$\csc \theta \equiv \frac{1}{\sin \theta} \equiv \sec \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\cot \theta}{\cos \theta} \,$

lunes, 1 de diciembre de 2014

Criterios de la Primera y Segunda Derivada

CRITERIO DE LA PRIMERA DERIVADA, UTILIZADO PARA UNA FUNCION CONTINUA Y SU PRIMERA DERIVADA TAMBIEN CONTINUA.

obtener la primera derivada.

igualar la primera derivada a cero y resolver la ecuación.

El valor o valores obtenidos para la variable, son donde pudiera haber máximos o mínimos en la función.

se asignan valores próximos (menores y mayores respectivamente) a la variable independiente y se sustituyen en la derivada. Se observan los resultados; cuando estos pasan de positivos a negativos, se trata de un punto máximo; si pasa de negativo a positivo el punto crítico es mínimo.

Cuando existen dos o más resultados para la variable independiente, debe tener la precaución de utilizar valores cercanos a cada uno y a la vez distante de los demás, a fin de evitar errores al interpretar los resultados.

sustituir en la función original (Y) el o los valores de la variable independiente (X) para los cuales hubo cambio de signo. Cada una de las parejas de datos así obtenidas, corresponde a las coordenadas de un punto crítico.

CRITERIO DE LA SEGUNDA DERIVADA

Este método es más utilizado que el anterior, aunque no siempre es más sencillo. Se basa en que en un máximo relativo, la concavidad de una curva es hacia abajo y en consecuencia, su derivada será negativa; mientras que en un punto mínimo relativo, la concavidad es hacia arriba y la segunda derivada es positiva.

Este procedimiento consiste en:

calcular la primera y segunda derivadas

igualar la primera derivada a cero y resolver la ecuación.

sustituir las raíces (el valor o valores de X) de la primera derivada en la segunda derivada.

Si el resultado es positivo, hay mínimo. Si la segunda derivada resulta negativa, hay un máximo.

Si el resultado fuera cero, no se puede afirmar si hay o no un máximo o mínimo.

sustituir los valores de las raíces de la primera derivada en la función original, para conocer las coordenadas de los puntos máximo y mínimo.

Sentido de Concavidad

En geometría, la concavidad de una curva o de una superficie es la parte que se asemeja a la zona interior de unacircunferencia o de una esfera, es decir, que tiene su parte hundida dirigida al observador. Es el concepto complementario al de convexidad.

Funciones Algebraicas Cóncavas

Una función es cóncava cuando dados dos puntos cualesquiera, el segmento que los une queda por debajo de la curva. Presenta su concavidad hacia abajo.³

La concavidad, como característica del gráfico de una función, se refiere a la condición geométrica de la región situada bajo una curva.

Se dice que una función f(x) es cóncava cuando la región bajo la curva también lo es, en caso que la función sea dos veces derivable, ésta es cóncava si y sólo si f"(x) < 0.

Una función cóncava, también se llama cóncava hacia abajo, mientras que una función convexa es llamada cóncava hacia arriba.

Aplicaciones de la Derivada : SENTIDO DE CONCAVIDAD DE UNA CURVA

Definición : Sea y = f (x) una curva plana , representada por la función f(x) , derivable.

• Se dice que f es Cóncava haciaarriba en el intervalo ]a , b[ , si todos los puntos de la gráfica quedan por encima de la tangente a la curva en un punto cualquiera en ese intervalo .

• Se dice que f es Cóncava hacia abajo enel intervalo ] a, b [ si todos los puntos de la gráfica quedan por debajo de la tangente a la curva en un punto cualquiera de ese intervalo.

Valores Criticos

El valor crítico se designa mediante z α/2.

P(Z > zα/2) = α/2

P[-z α/2 < z < z α/2] = 1 − α

α es rl nivel de significación.

1 − α es el nivel de confianza, que es la probabilidad de que el parámetro a estimar se encuentre en el intervalo de confianza.

Los niveles de confianza más usuales son: 90%; 95% y 99%.

Bilateral

1 - α	α/2	z_α/2
0.90	0.05	1.645
0.95	0.025	1.96
0.99	0.005	2.575

Unilateral

1 - α	α	z_α
0.90	0.10	1.28
0.95	0.05	1.645
0.99	0.01	2.33

Punto de Inflexión

Un punto de inflexión es un punto donde los valores de x de una función continua pasa de un tipo de concavidad a otra. La curva "atraviesa" la tangente. Matemáticamente la derivada segunda de la función f en el punto de inflexión es cero, o no existe.

En el cálculo de varias variables a estos puntos de inflexión se les conoce como puntos de ensilladura.

En las funciones derivables reales de una variable real, para hallar estos puntos de inflexión, basta con igualar la segunda derivada de la función a cero y despejar. Los puntos obtenidos deberán ser sustituidos en la derivada tercera o sucesivas hasta que nos dé un valor diferente de cero. Cuando esto suceda, si la derivada para la que es distinto de cero es impar, se trata de un punto de inflexión; pero, si se trata de derivada par, no lo es. Más concretamente:
Se halla la primera derivada de

Se halla la segunda derivada de

Se halla la tercera derivada de

Se iguala la segunda derivada a 0:

Se despeja la variable independiente y se obtienen todos los valores posibles de la misma:

.
Se halla la imagen de cada

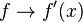
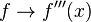
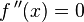
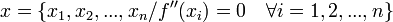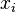sustituyendo la variable dependiente en la función.
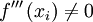Ahora, en la tercera derivada, se sustituye cada

:
Si

, se tiene un punto de inflexión en

.
Si

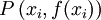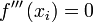, debemos sustituir

en las sucesivas derivadas hasta sea distinto de cero. Cuando se halle la derivada para la que

no sea nulo, hay que ver qué derivada es:
Si la derivada es impar, se trata de un punto de inflexión.
Si la derivada es par, no se trata de un punto de inflexión.

La ecuación

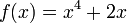no tiene puntos de inflexión, porque la derivada segunda es siempre mayor o igual a cero, por tanto no hay cambio de concavidad dado que es no negativa en todo su dominio. Sin embargo en

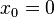la derivada segunda se anula y la primera derivada no nula en

es la derivada cuarta, que es par. Obsérvese que

tampoco presenta un extremo en

Definicion de Maximos,Minimos,Absolutas y Relativas

Máximo absoluto

Una función tiene su máximo absoluto en el x = a si la ordenada es mayor o igual que en cualquier otro punto del dominio de la función.

Sea f una función de valores reales definida en un conjunto S de números reales. Se dice que la función f tiene un máximo absoluto en el conjunto S si existe por lo menos un punto c en S tal que
f(x)≤f(c) para todo x en S
El número f(c) se llama máximo absoluto de f en S.

Mínimo absoluto

Una función tiene su mínimo absoluto en el x = b si la ordenada es menor o igual que en cualquier otro punto del dominio de la función.

Para una función con las mismas características que la definida en el máximo absoluto, se dice que f tiene un mínimo absoluto en S si existe un punto d en S tal que
f(x)≥f(d) para todo x en S

Maximo relativo

Una función f tiene un máximo relativo en el punto a, si f(a) es mayor o igual que los puntos próximos al punto a.

Una función f, definida en un conjunto S, tiene un máximo relativo en un punto c de S si existe un cierto intervalo abierto I que contiene c tal que
f(x)≤f(x) para todo x situado en I∩S

Minimo relativo

Una función f tiene un mínimo relativo en el punto b, si f(b) es menor o igual que los puntos próximos al punto b.

La definicón de mínimo relativo se formula igual que la de máximo relativo, pero cambiando la desigualdad.

Definición de Derivadas

En matemáticas, la derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado.

La derivada, por lo tanto, representa cómo se modifica una función a medida que su entrada también registra alteraciones. En los casos de las funciones de valores reales de una única variable, la derivada representa, en un cierto punto, el valor de la pendiente de la recta tangente al gráfico de la función en dicho punto.

martes, 7 de octubre de 2014

Condiciones de Continuidad

Una función continua es aquella cuya regla de correspondencia asigna incrementos pequeños en la variable dependiente a pequeños incrementos de los elementos del dominio de dicha función, es decir, , y usando la expresión Δy + y = f(Δx + x), queda donde en este caso, f(x) = y. Ello quiere decir que , y si este último límite existe significa en consecuencia por un teorema de límites (un límite existe si y sólo si los dos límites laterales existen y son iguales) que toda función f(x) que cumpla con
es continua en el punto a.Condición no recíproca La relación no funciona a la inversa: el que una función sea continua no garantiza su derivabilidad. Es posible que los límites laterales sean equivalentes pero las derivadas laterales no; en este caso la función presenta un punto anguloso en dicho punto.Un ejemplo puede ser la función valor absoluto (también llamada módulo) en el punto . Dicha función es equivalente a la función partida Para valores infinitamente cercanos a 0, por ambas ramas, el resultado tiende a 0. Y el resultado en el punto 0 es también 0, por lo tanto es continua. Sin embargo, las derivadas resultan Cuando vale 0, las derivadas laterales dan resultados diferentes. Por lo tanto, no existe derivada en el punto, a pesar de que sea continuo.De manera informal, si el gráfico de la función tiene puntas agudas, se interrumpe o tiene saltos, no es derivable.

Tipos de Limites

1) LIMITE EN UN PUNTO.

a) Límite finito:
Se dice que la función y = f(x) tiene por límite l cuando x tiende hacia a, y se representa por

(Es decir, que si fijamos un entorno de l de radio
, podemos encontrar un entorno de a de radio
, que depende de
, de modo que para cualquier valor de x que esté en el entorno E(a,
) exceptuando el propio a, se tiene que su imagen f(a) está en el entorno E(l,
).)