Una función continua es aquella cuya regla de correspondencia asigna incrementos pequeños en la variable dependiente a pequeños incrementos de los elementos del dominio de dicha función, es decir, , y usando la expresión Δy + y = f(Δx + x), queda donde en este caso, f(x) = y. Ello quiere decir que , y si este último límite existe significa en consecuencia por un teorema de límites (un límite existe si y sólo si los dos límites laterales existen y son iguales) que toda función f(x) que cumpla con
es continua en el punto a.Condición no recíproca La relación no funciona a la inversa: el que una función sea continua no garantiza su derivabilidad. Es posible que los límites laterales sean equivalentes pero las derivadas laterales no; en este caso la función presenta un punto anguloso en dicho punto.Un ejemplo puede ser la función valor absoluto (también llamada módulo) en el punto . Dicha función es equivalente a la función partida Para valores infinitamente cercanos a 0, por ambas ramas, el resultado tiende a 0. Y el resultado en el punto 0 es también 0, por lo tanto es continua. Sin embargo, las derivadas resultan Cuando vale 0, las derivadas laterales dan resultados diferentes. Por lo tanto, no existe derivada en el punto, a pesar de que sea continuo.De manera informal, si el gráfico de la función tiene puntas agudas, se interrumpe o tiene saltos, no es derivable.
martes, 7 de octubre de 2014
Tipos de Limites
1) LIMITE EN UN PUNTO.
a) Límite finito:
Se dice que la función y = f(x) tiene por límite l cuando x tiende hacia a, y se representa por

(Es decir, que si fijamos un entorno de l de radio
, podemos encontrar un entorno de a de radio
, que depende de
, de modo que para cualquier valor de x que esté en el entorno E(a,
) exceptuando el propio a, se tiene que su imagen f(a) está en el entorno E(l,
).)
Se dice que la función y = f(x) tiene por límite l cuando x tiende hacia a, y se representa por
(Es decir, que si fijamos un entorno de l de radio
, podemos encontrar un entorno de a de radio
, que depende de
, de modo que para cualquier valor de x que esté en el entorno E(a,
) exceptuando el propio a, se tiene que su imagen f(a) está en el entorno E(l,
).)
b) Límite infinito: (A partir de ahora usaremos la notación matemática para hacer más corta la definición). 
.
.
c) Límite por la izquierda: 
d) Límite por la derecha: 
2) PROPIEDADES O REGLAS DE LOS LÍMITES.
a) 
siempre que no aparezca la indeterminación
.
siempre que no aparezca la indeterminación
.
b) 
con
.
con
.
c) 
siempre y cuando no aparezca la indeterminación
.
siempre y cuando no aparezca la indeterminación
.
d) 
siempre y cuando no aparezcan las indeterminaciones
e
.

siempre y cuando no aparezcan las indeterminaciones
e
.
e) 
con
, siempre y cuando tengan sentido las potencias que aparecen.
con
, siempre y cuando tengan sentido las potencias que aparecen.
f) 
siempre y cuando tengan sentido las potencias que aparecen y no nos encontremos con indeterminaciones de los tipos
.
siempre y cuando tengan sentido las potencias que aparecen y no nos encontremos con indeterminaciones de los tipos
.
Definicion de Limite
En matemática, el concepto de límite es una noción topológica que formaliza la noción intuitiva de aproximación hacia un punto concreto de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor.
En cálculo infinitesimal (especialmente en análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación, integración, entre otros. Si bien, el concepto de límite parece intuitivamente relacionado con el concepto de distancia, en un espacio euclídeo, es la clase de conjuntos abiertos inducidospor dicha métrica, lo que permite definir rigurosamente la noción de límite.
El concepto se puede generalizar a otros espacios topológicos, como pueden ser las redes topológicas; de la misma manera, es definido y utilizado en otras ramas de la matemática, como puede ser la teoría de categorías.
Para fórmulas, el límite se utiliza usualmente de forma abreviada mediante lim como en lim(an) = a o se representa mediante la flecha (→) como en an → a.
Límite de una función
En análisis real para funciones de una variable, se puede hacer una definiciónde límite similar a la de límite de una sucesión, en la cual, los valores que toma la función dentro de un intervalo o radio de convergencia se van aproximando a un punto fijado c, independientemente de que éste pertenezca al dominio de la función. El punto c es punto de acumulación del dominio de la función. Esto se puede generalizar aún más a funciones de varias variables o funciones en distintos espacios métricos
Informalmente, se dice que el límite de la función f(x) es L cuando x tiende ac, y se escribe:
Límite de una sucesión de conjuntos
En teoría de conjuntos también se utiliza el concepto de límite, que se puede calcular sobre una sucesión de conjuntos. Para ello, los conjuntos deben de cumplir una serie de condiciones, como puede ser la monotonía (creciente o decreciente). De manera más general, y utilizando la definición de límite superior y límite inferior para una sucesión de conjuntos cualquiera 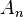 , se dice que el límite de esta sucesión existe si el límite superior y límite inferior existen y son iguales. En general se tiene:
, se dice que el límite de esta sucesión existe si el límite superior y límite inferior existen y son iguales. En general se tiene:

Si el límite primer término y el penúltimo son iguales entonces se verifican todas las igualdades. Estos conceptos son muy útiles en disciplinas de las matemáticas como la teoría de la medida, especialmente en espacios de probabilidad. No es difícil construir sucesiones no convergentes donde se verifica que:
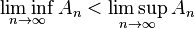
Suscribirse a:
Comentarios (Atom)

