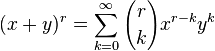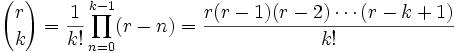Primero que nada iniciemos con un breve pedazo de su biografia en el desarrollo del calculo.
De 1667 a 1669 emprendió investigaciones sobre óptica y fue elegido fellow del Trinity College. En 1669, su mentor, Isaac Barrow, renunció a su Cátedra Lucasiana de matemática, puesto en el que Newton le sucedería hasta 1696. El mismo año envió a John Collins, por medio de Barrow, su Analysis per aequationes número terminorum infinitos. Para Newton, este manuscrito representa la introducción a un potente método general, que desarrollaría más tarde: su cálculo diferencial eintegral.
Newton había descubierto los principios de su cálculo diferencial e integral hacia 1665-1666 y, durante el decenio siguiente, elaboró al menos tres enfoques diferentes de su nuevo análisis.
Newton y Leibniz protagonizaron una agria polémica sobre la autoría del desarrollo de esta rama de la matemática. Los historiadores de la ciencia consideran que ambos desarrollaron el cálculo independientemente, si bien la notación de Leibniz era mejor y la formulación de Newton se aplicaba mejor a problemas prácticos. La polémica dividió aún más a los matemáticos británicos y continentales. Sin embargo esta separación no fue tan profunda como para que Newton y Leibniz dejaran de intercambiar resultados.
Newton abordó el desarrollo del cálculo a partir de la geometría analítica desarrollando un enfoque geométrico y analítico de las derivadas matemáticas aplicadas sobre curvas definidas a través de ecuaciones. Newton también buscaba cómo cuadrar distintas curvas, y la relación entre la cuadratura y la teoría de tangentes. Después de los estudios de Roberval, Newton se percató de que el método de tangentes podía utilizarse para obtener las velocidades instantáneas de una trayectoria conocida. En sus primeras investigaciones Newton lidia únicamente con problemas geométricos, como encontrar tangentes, curvaturas y áreas utilizando como base matemática la geometría analítica de Descartes. No obstante, con el afán de separar su teoría de la de Descartes, comenzó a trabajar únicamente con las ecuaciones y sus variables sin necesidad de recurrir al sistema cartesiano.
Investigaciones de Isaac Newton.
Desde finales de 1664 trabajó intensamente en diferentes problemas matemáticos.
Abordó entonces el teorema del binomio.
Teorema generalizado del binomio (Newton)
Isaac Newton generalizó la fórmula para tomar otros exponentes, considerando una serie infinita:
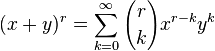
Donde r puede ser cualquier número complejo (en particular, r puede ser cualquier número real, no necesariamente positivo ni entero), y los coeficientes están dados por: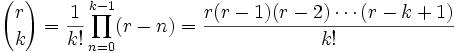 
De 1667 a 1669 emprendió investigaciones sobre óptica y fue elegido fellow del Trinity College.
En 1669 su mentor, Isaac Barrow, renunció a su Cátedra Lucasiana de matemática, puesto en el que Newton le sucedería hasta 1696.
Descubrimiento de las series de sin x y cos x
A partir de su binomio, Newton encuentra también series trigonométricas. Si consideramos la circunferencia de radio 1, de acuerdo con
la figura
es x=AQ=sin q, esto es, q= arcsinx, de manera que
| q = 2 ·área(OQR)=2 ·[área(ORQB)-área(OQB)] = |
|
Por el desarrollo del binomio
de donde integrando término a término
mientra que
sustituyendo y después de simplificar queda
| q = x+ | 1
6 | x3+ | 3
40 | x5+ | 5
112 | x7+  |
|
Inviertiendo ahora la serie Newton obtiene
| x=sinq = q- | 1
6 | q3+ | 1
120 | q5- | 1
5040 | q7+ |
|
Encuentra luego la serie de cosq como
y calcula las cuadraturas de la cicloide y luego de la cuadratriz, de ecuación x=y coty primero invirtiendo esta ecuación para encontrar la
serie de y=y(x) y luego integrando término a término.
El método de Fluxiones.
Newton da luego otra versión de su cálculo en "Methodus Fluxiorum et Serierum Infinitorum" que fue escrito en 1671 y publicado
en 1736. Wallis, con permiso de Newton, incluyó el método de fluxiones en la páginas 390-396 de su Algebra.
Newton concibe las cantidades matemáticas como el movimiento continuo de un punto que traza una curva. Cada una de estas cantidades
que aparecen (variable) x es un "fluente" y su velocidad, designada por 
, esto es una x con un puntito encima, es una "fluxión".
La parte infinitesimal pequeña en la que un fluente se incrementa por unidad de tiempo o, es o el momento del fluente. El problema
fundamental es, dada una relación entre fluentes hallar la relación entre sus fluxiones y recíprocamente. Si y=f(x) en un pequeño
intervalo o de tiempo x se incrementa a x+o, y se incrementa a
Al ser
| y+o |
.
y
| =f(x+o |
| ) se tiene o |
.
y
| =f(x+o |
| )-f(x) |
|
es decir
Veamos como hace Newton en un caso concreto. Si es y=x3 obtenemos
Luego elimina los términos que contienen o, ya que "se le supone infinitamente pequeño", quedando
y por tanto, la relación entre fluxiones es
De esta forma su afirmación inicial del párrafo anterior de que el área
proviene de la curva y=xn es que el cociente de fluxiones
considerando luego que la fluxión de x es uno, es decir, que el incremento que considera en x por unidad de tiempo es uno.
Aplica también su método al caso de tener dada una curva en la forma f(x,y)=0. Por ejemplo considera el caso de la cúbica
Sustituye x por x+
o e y por y+
o, realiza el desarrollo, resta la relación x3-ax2+axy-y3=0, cancela los términos con o2 y o3 por ser despreciables frente a o, y divide ahora por o para obtener
| 3x2 |
| -2a x |
| +ay |
| +ax |
.
y
| -3y2 |
.
y
| =0 |
|
de donde obtiene la relación de fluxiones
Newton es consciente de las dificultades de rigor que tienen estos conceptos y posteriormente refina su interpretación en "De Quadratura Curvarum" , escrito en 1676 y publicado en 1704. Aquí habla de "últimas proporciones" ( "ultimate ratios" ). Dice: "Por última proporción de cantidades evanescentes debemos entender el cociente de estas cantidades, no antes de que desvanezcan, ni después, pero tal como van desvaneciendo."
Intuitivamente, esto viene a ser nuestro concepto de derivada interpretada como límite
| f¢(x)= |
lim
h®0 | | f(x+h)-f(x)
h | |
|
Cálculo de Newton del número π
Aparece en su "Methodus Fluxiorum et Serierum Infinitorum," 1671. Newton considera la circunferencia de centro (1/2,0) y radio 1/2
de donde despejando y en función de x y usando el desarrollo del binomio
| y=x1/2(1-x)1/2=x1/2 | ( | 1- | x
2 | - | x2
8 | - | x3
16 | - | 5
128 | x4- | 7
256 | x5- | ) | = |
|
| = x1/2- | 1
2 | x3/2- | 1
8 | x5/2- | 5
128 | x9/2- | 7
256 | x11/2- |
|
Calcula entonces el área debajo de la curva integrando término a término
| A(x)= | 2
3 | x3/2- | 1
5 | x5/2- | 1
28 | x7/2- | 1
72 | x9/2- | 5
704 | x11/2- |
|
Luego para x=1/4, el área de la región ADB es igual a
| área (ADB)= | 1
12 | - | 1
160 | - | 1
3584 | - | 1
36864 | - | 5
1441792 | - = 0.076663 |
|
Calcula luego la misma área por geometría, ya que
| área (ADB)= área(sectorACD)-área(triánguloDBC) |
|
Para evaluar esta última relación calcula primero
Luego se observa de los lados del triángulo BCD que el ángulo en C es de 60o. De donde
| área(sectorACD)= | 1
3 | área(semicircunferencia) |  | | |
|
Mientras que
Por tanto
Igualando los dos valores encontrados anteriormente para esta área resulta
y por consiguiente
valor que aquí hemos calculado correcto hasta cuatro decimales (el error es 1.33 x10-5). Newton de hecho usa 20 términos del binomio para llegar a calcular p con 16 decimales correctos.
Luego dice "I am ashamed to tell you how many figures I carried these calculations, having no other business at the time" (Me avergüenzo de decirle cuantas cifras he calculado, no teniendo nada más que hacer en aquél momento). A pesar de sus afirmaciones, este es un nuevo paso de gigante en el
cálculo del númerop.
